Tartalom

• Lépések
• Módszer 1 /3: Hogyan oldjuk meg a köbös egyenletet állandó tag nélkül
• 2. módszer a 3 -ból: Hogyan keressünk egész gyökereket szorzók segítségével
• 3. módszer a 3 -ból: Hogyan oldjunk meg egyenletet a diszkrimináns segítségével

Egy köbös egyenletben a legnagyobb kitevő 3, egy ilyen egyenletnek 3 gyöke (megoldása) és formája ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Egyes köbös egyenleteket nem olyan könnyű megoldani, de ha a megfelelő módszert alkalmazza (jó elméleti háttérrel), megtalálhatja a legösszetettebb köbös egyenlet gyökereit is - ehhez használja a másodfokú egyenlet megoldásának képletét egész gyökerek, vagy számítsuk ki a diszkriminánst.

Lépések

Módszer 1 /3: Hogyan oldjuk meg a köbös egyenletet állandó tag nélkül

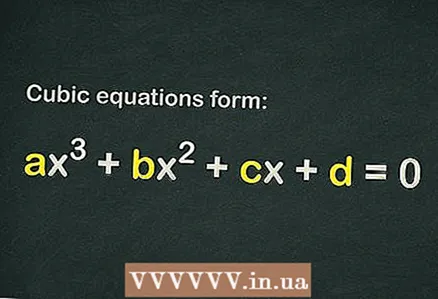1. 1 Tudja meg, hogy van -e szabad kifejezés a köbös egyenletben d{ displaystyle d}. A köbös egyenlet alakja ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Ahhoz, hogy egy egyenletet köbösnek lehessen tekinteni, elegendő, ha csak a kifejezést ${ displaystyle x ^ {3}}$ (vagyis lehet, hogy egyáltalán nincsenek más tagok).
   • Ha az egyenletnek van szabad tagja ${ displaystyle d}$, használjon más módszert.
   • Ha az egyenletben ${ displaystyle a = 0}$, nem köbös.
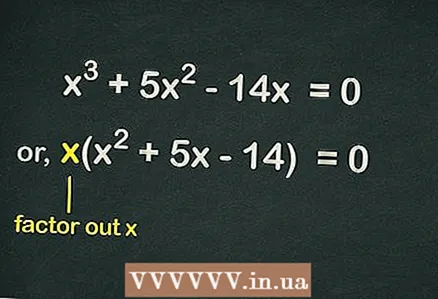2. 2 Vegye ki a zárójelekből x{ displaystyle x}. Mivel az egyenletben nincs szabad kifejezés, az egyenlet minden tagja tartalmazza a változót ${ displaystyle x}$... Ez azt jelenti, hogy az egyik ${ displaystyle x}$ zárójelből ki lehet zárni az egyenlet egyszerűsítése érdekében. Így az egyenletet így írjuk fel: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Például adott egy köbös egyenlet ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Vegye ki ${ displaystyle x}$ zárójelek és kap ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
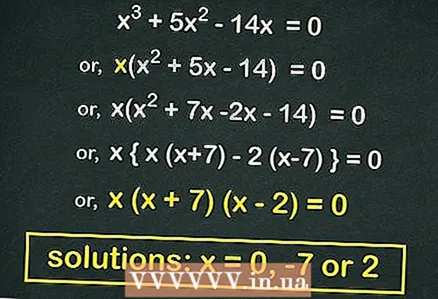3. 3 Faktor (két binomiális szorzat) a másodfokú egyenlet (ha lehetséges). A forma sok másodfokú egyenlete ${ displaystyle ax ^ {2} + bx + c = 0}$ faktorizálható. Egy ilyen egyenlet kiderül, ha kivesszük ${ displaystyle x}$ a zárójeleken kívül. Példánkban:
   • Vegye ki a zárójelekből ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • A másodfokú egyenlet tényezője: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Egyenlítsen minden tartályt ehhez ${ displaystyle 0}$... Ennek az egyenletnek a gyökerei ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Oldja meg a másodfokú egyenletet egy speciális képlet segítségével. Tegye ezt, ha a másodfokú egyenletet nem lehet faktorizálni. Egy egyenlet két gyökének, az együtthatók értékeinek megkereséséhez ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ helyettesíti a képletben ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Példánkban helyettesítsük az együtthatók értékeit ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) a képletbe:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Első gyökér:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Második gyökér:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Használjon nulla és másodfokú gyököket a köbös egyenlet megoldásaként. A másodfokú egyenleteknek két gyökere van, míg a köbös egyenleteknek három. Már két megoldást talált - ezek a másodfokú egyenlet gyökerei. Ha az "x" -et a zárójeleken kívülre teszi, a harmadik megoldás az lenne ${ displaystyle 0}$.
   • Ha "x" -et vesz ki a zárójelekből, akkor kap ${ displaystyle x (ax ^ {2} + bx + c) = 0}$vagyis két tényező: ${ displaystyle x}$ és másodfokú egyenlet zárójelben. Ha ezen tényezők bármelyike ​​az ${ displaystyle 0}$, az egész egyenlet is egyenlő ${ displaystyle 0}$.
   • Így a másodfokú egyenlet két gyöke egy köbös egyenlet megoldása. A harmadik megoldás az ${ displaystyle x = 0}$.

2. módszer a 3 -ból: Hogyan keressünk egész gyökereket szorzók segítségével

1. 1 Győződjön meg arról, hogy van egy szabad kifejezés a köbös egyenletben d{ displaystyle d}. Ha a forma egyenletében ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ van szabad tag ${ displaystyle d}$ (ami nem egyenlő a nullával), nem fog működni, ha az "x" -et a zárójeleken kívülre helyezi. Ebben az esetben használja az ebben a szakaszban ismertetett módszert.
   • Például adott egy köbös egyenlet ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Ha nullát szeretne kapni az egyenlet jobb oldalán, adja hozzá ${ displaystyle 6}$ az egyenlet mindkét oldalára.
   • Majd kiderül az egyenlet ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Mint ${ displaystyle d = 6}$, az első részben leírt módszer nem használható.
2. 2 Írja le az együttható tényezőit! a{ displaystyle a} és szabad tag d{ displaystyle d}. Vagyis keresse meg a szám tényezőit a címen ${ displaystyle x ^ {3}}$ és számok az egyenlőségjel előtt. Emlékezzünk vissza, hogy egy szám tényezői azok a számok, amelyek megszorozva azt a számot eredményezik.
   • Például, hogy megkapja a számot 6, szaporodnia kell ${ displaystyle 6 alkalommal 1}$ és ${ displaystyle 2 x 3}$... Tehát a számok 1, 2, 3, 6 a szám tényezői 6.
   • Az egyenletünkben ${ displaystyle a = 2}$ és ${ displaystyle d = 6}$... Szorzók 2 vannak 1 és 2... Szorzók 6 a számok 1, 2, 3 és 6.
3. 3 Oszd el az egyes tényezőket a{ displaystyle a} minden tényezőre d{ displaystyle d}. Ennek eredményeként sok törtet és több egész számot kap; a köbös egyenlet gyöke az egész számok egyike vagy az egyik egész negatív értéke.
   • Példánkban osszuk el a tényezőket ${ displaystyle a}$ (1 és 2) tényezők szerint ${ displaystyle d}$ (1, 2, 3 és 6). Fogsz kapni: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ és ${ displaystyle { frac {2} {3}}}$... Most adja hozzá a kapott törtek és számok negatív értékeit ehhez a listához: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ és ${ displaystyle - { frac {2} {3}}}$... A köbös egyenlet egész gyöke néhány szám ebből a listából.
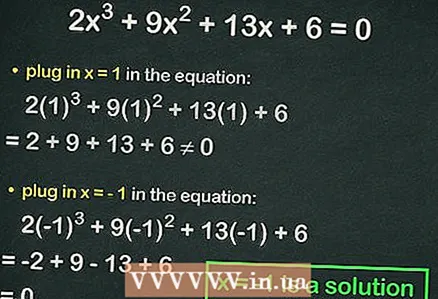4. 4 Dugjon be egész számokat a köbös egyenletbe. Ha az egyenlőség igaz, akkor a helyettesített szám az egyenlet gyöke. Például helyettesítse az egyenletet ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, azaz nem tartják be az egyenlőséget. Ebben az esetben írja be a következő számot.
   • Helyettes ${ displaystyle -1}$: ${ displaystyle (-2) +9 +(- 13) +6}$ = 0. Így, ${ displaystyle -1}$ az egyenlet teljes gyöke.
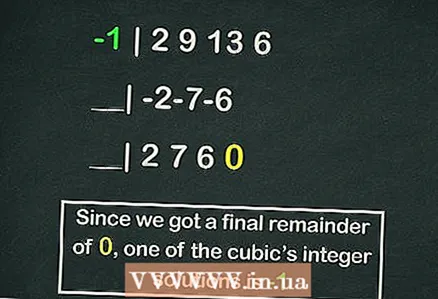5. 5 Használja a polinomok osztásának módszerét Horner sémájahogy gyorsabban megtaláljuk az egyenlet gyökereit. Tegye ezt, ha nem akarja manuálisan helyettesíteni a számokat az egyenletben. Horner sémájában az egész számokat el kell osztani az egyenlet együtthatóinak értékeivel ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ és ${ displaystyle d}$... Ha a számok egyenletesen oszthatók (vagyis a maradék ${ displaystyle 0}$), egy egész szám az egyenlet gyöke.
   • Horner sémája külön cikket érdemel, de az alábbi példa a köbös egyenletünk egyik gyökének kiszámítására szolgál ezzel a sémával:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Tehát a többi az ${ displaystyle 0}$, de ${ displaystyle -1}$ az egyenlet egyik gyökere.

3. módszer a 3 -ból: Hogyan oldjunk meg egyenletet a diszkrimináns segítségével

1. 1 Írja le az egyenlet együtthatóinak értékeit a{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} és d{ displaystyle d}. Javasoljuk, hogy a megadott együtthatók értékeit előre írja le, hogy a jövőben ne zavarodjon össze.
   • Például, ha megadjuk az egyenletet ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... Írd le ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ és ${ displaystyle d = -1}$... Emlékezz vissza, ha korábban ${ displaystyle x}$ nincs szám, a megfelelő együttható továbbra is fennáll és egyenlő ${ displaystyle 1}$.
2. 2 Számítsa ki a nulla diszkriminánst egy speciális képlet segítségével. Ahhoz, hogy a köbös egyenletet a diszkrimináns segítségével megoldhassuk, számos nehéz számítást kell elvégeznünk, de ha minden lépést helyesen hajtunk végre, ez a módszer nélkülözhetetlen lesz a legösszetettebb köbös egyenletek megoldásához. Első számítás ${ displaystyle Delta _ {0}}$ (nulla diszkrimináns) az első érték, amire szükségünk van; Ehhez cserélje ki a megfelelő értékeket a képletben ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • A diszkrimináns egy szám, amely a polinom gyökereit jellemzi (például a másodfokú egyenlet diszkriminánsát a képlet számítja ki ${ displaystyle b ^ {2} -4ac}$).
   • Egyenletünkben:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Számítsa ki az első megkülönböztetőt a képlet segítségével Δ1=2b3−9abc+27a2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Az első diszkrimináns ${ displaystyle Delta _ {1}}$ - ez a második fontos érték; kiszámításához csatlakoztassa a megfelelő értékeket a megadott képlethez.
   • Egyenletünkben:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Kiszámítja:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Vagyis keresse meg a köbös egyenlet megkülönböztetőjét a kapott értékeken keresztül ${ displaystyle Delta _ {0}}$ és ${ displaystyle Delta _ {1}}$... Ha a köbös egyenlet diszkriminánsa pozitív, akkor az egyenletnek három gyöke van; ha a diszkrimináns nulla, akkor az egyenletnek egy vagy két gyöke van; ha a diszkrimináns negatív, akkor az egyenletnek egy gyöke van.
   • Egy köbös egyenletnek mindig van legalább egy gyöke, mivel ennek az egyenletnek a gráfja legalább egy pontban metszi az X tengelyt.
   • Az egyenletünkben ${ displaystyle Delta _ {0}}$ és ${ displaystyle Delta _ {1}}$ egyenlőek ${ displaystyle 0}$, így könnyen kiszámíthatja ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Így egyenletünknek egy vagy két gyökere van.

5. 5 Kiszámítja:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } jobb) div 2}}}$. ${ displaystyle C}$ - ez az utolsó fontos mennyiség, amelyet meg kell találni; segít kiszámítani az egyenlet gyökereit. Helyezze be az értékeket a megadott képletbe ${ displaystyle Delta _ {1}}$ és ${ displaystyle Delta _ {0}}$.
   • Egyenletünkben:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Keresse meg az egyenlet három gyökét! Csináld a képlettel ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, ahol ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, de n egyenlő 1, 2 vagy 3... Cserélje ki a megfelelő értékeket ebbe a képletbe - ennek eredményeként három egyenletet kap.
   • Számítsa ki az értéket a következő képlet segítségével: n = 1, 2 vagy 3majd ellenőrizze a választ. Ha a válasz ellenőrzésekor 0 -t kap, akkor ez az érték az egyenlet gyökere.
   • Példánkban helyettesítő 1 ban ben ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ és kap 0, azaz 1 az egyenlet egyik gyökere.