Tartalom

• Lépni
• 1/4 rész: A mátrix elkészítése
• 4. rész: A rendszer mátrixos megoldásának műveleteinek megtanulása
• 4. rész: Összeolvasztja a galaxis megoldásának lépéseit
• 4/4 rész: A megoldás ellenőrzése
• Tippek

A mátrix nagyon hasznos módszer a számok blokk formátumban való ábrázolására, amelyet ezután felhasználhat egy lineáris egyenletrendszer megoldására. Ha csak két változója van, akkor valószínűleg más módszert fog használni. Olvassa el erről az egyenletrendszer megoldása példákat ezekre a más módszerekre. De ha három vagy több változója van, akkor egy tömb ideális. A szorzás és összeadás ismételt kombinációinak alkalmazásával szisztematikusan eljuthat a megoldásig.

Lépni

1/4 rész: A mátrix elkészítése

1. Ellenőrizze, hogy rendelkezik-e elegendő adattal. Ahhoz, hogy egy lineáris rendszer minden változójára egyedi megoldást kapjon egy mátrix segítségével, annyi egyenletre van szüksége, mint ahány változót megpróbál megoldani. Például: az x, y és z változókkal három egyenletre van szükség. Ha négy változója van, akkor négy egyenletre van szüksége.
   • Ha kevesebb egyenleted van, mint a változók száma, akkor megtudod a változók néhány határát (például x = 3y és y = 2z), de nem tudsz pontos megoldást találni. Ebben a cikkben csak egy egyedi megoldás kidolgozásán fogunk dolgozni.
2. Írja be az egyenleteit a szokásos formába. Mielőtt az egyenletek adatait mátrix formába helyezheti, először minden egyes egyenletet szabványos formában kell megírnia. A lineáris egyenlet szokásos alakja Ax + By + Cz = D, ahol a nagybetűk az együtthatók (számok), az utolsó szám (ebben a példában D) az egyenlőségjeltől jobbra vannak.
   • Ha több változója van, csak addig folytassa a sort, amíg szükséges. Például, ha hat változóval próbálta megoldani a rendszert, akkor az alapértelmezett alakja úgy néz ki, mint Au + Bv + Cw + Dx + Ey + Fz = G. Ebben a cikkben azokra a rendszerekre fogunk összpontosítani, amelyek csak három változóval rendelkeznek. Egy nagyobb galaxis megoldása pontosan ugyanaz, de csak több időt és több lépést igényel.
   • Ne feledje, hogy szabványos formában a kifejezések közötti műveletek mindig kiegészítést jelentenek. Ha van egy kivonás az egyenletedben, az összeadás helyett ezzel később kell dolgoznod azzal, hogy negatívvá teszed az együtthatót. Ennek könnyebb megjegyzése érdekében átírhatja az egyenletet, hozzáadhatja a műveletet, és negatívvá teheti az együtthatót. Például átírhatja a 3x-2y + 4z = 1 egyenletet 3x + (- 2y) + 4z = 1 értékre.
3. Helyezze az egyenletrendszer számait egy mátrixba. A mátrix egy számcsoport, egyfajta táblába rendezve, amellyel a rendszer megoldásán fogunk dolgozni. Alapvetően ugyanazokat az adatokat tartalmazza, mint maguk az egyenletek, de egyszerűbb formátumban. Az egyenletek mátrixának szabványos formában történő elkészítéséhez egyszerűen másolja az egyes egyenletek együtthatóit és eredményeit egyetlen sorba, és halmozza ezeket a sorokat egymásra.
   • Tegyük fel, hogy van egy rendszere, amely a három egyenletből áll: 3x + y-z = 9, 2x-2y + z = -3 és x + y + z = 7. A mátrixod legfelső sora a 3, 1, -1, 9 számokat fogja tartalmazni, mivel ezek az együtthatók és az első egyenlet megoldása. Vegye figyelembe, hogy minden változónak, amelynek nincs együtthatója, feltételezzük, hogy annak együtthatója 1. A mátrix második sora 2, -2, 1, -3, a harmadik sor pedig 1, 1, 1, 7 lesz.
   • Ügyeljen arra, hogy az első oszlopban az x, a másodikban az y együtthatókat, a harmadikban a z együtthatókat, a negyedikben pedig a megoldási feltételeket igazítsa. Ha végzett a mátrixszal, ezek az oszlopok fontosak lesznek a megoldás megírásakor.
4. Rajzoljon egy nagy szögletes zárójelet a teljes mátrix köré. Megállapodás szerint a mátrixot szögletes zárójelekkel [] jelöljük a teljes számblokk körül. A zárójelek semmilyen módon nem befolyásolják a megoldást, de azt jelzik, hogy mátrixokkal dolgozol. A mátrix tetszőleges számú sorból és oszlopból állhat. Ebben a cikkben zárójeleket fogunk használni a kifejezések körül egymás után, jelezve, hogy összetartoznak.
5. A közös szimbolika használata. Ha mátrixokkal dolgozunk, gyakran hivatkozunk az R rövidítéssel ellátott sorokra és a C rövidítéssel ellátott oszlopokra. Ezekkel a betűkkel együtt számokat is használhat egy adott sor vagy oszlop megjelölésére. Például egy mátrix 1. sorának jelzéséhez írhat R1-et. A 2. sorból ezután R2 lesz.
   • A mátrix bármely konkrét helyzetét R és C kombinációjával jelezheti. Például a második sor, harmadik oszlopban egy kifejezés megjelölésére R2C3-nak nevezheti.

4. rész: A rendszer mátrixos megoldásának műveleteinek megtanulása

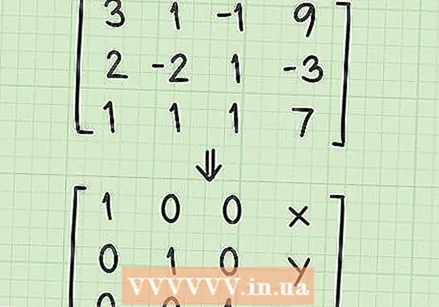1. Értse meg az oldatmátrix alakját. Mielőtt elkezdené megoldani az egyenletrendszert, meg kell értenie, hogy mit fog kezdeni a mátrixszal. Ezen a ponton van egy mátrixod, amely így néz ki:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • Számos alapvető művelettel dolgozik a "megoldási mátrix" létrehozásában. A megoldásmátrix így fog kinézni:
   • 1 0 0 x
   • 0 1 0 y
   • 0 0 1 z
   • Vegye figyelembe, hogy a mátrix átlós vonalban 1-ből áll, a negyedik oszlop kivételével az összes többi térben 0-val. A negyedik oszlopban szereplő számok jelentik a megoldást az x, y és z változókra.
2. Használjon skaláris szorzást. Az első eszköz, amely a rendszer mátrix segítségével történő megoldására szolgál, a skaláris szorzás. Ez egyszerűen egy kifejezés, ami azt jelenti, hogy a mátrix egy sorában lévő elemeket megszorozzuk konstans számmal (nem változóval). Ha skaláris szorzást használ, ne feledje, hogy a teljes sor minden tagját meg kell szoroznia a kiválasztott számmal. Ha elfelejti az első kifejezést, és csak szaporodik, akkor rossz megoldást kap. Azonban nem kell egyszerre megszoroznia a teljes mátrixot. Skaláris szorzásban egyszerre csak egy soron dolgozik.
   • Gyakori a törtek használata a skaláris szorzásban, mert gyakran 1-es átlós sort szeretne kapni. Szokja meg a törtekkel való munkát. Könnyebb lesz (a mátrix megoldásának legtöbb lépésében), ha nem megfelelő formában tudja megírni a frakcióit, majd visszaalakítja vegyes számokká a végső megoldáshoz. Ezért az 1 2/3 számmal könnyebben lehet dolgozni, ha azt 5/3 -nak írjuk.
   • Például példaproblémánk első sora (R1) a [3,1, -1,9] kifejezésekkel kezdődik. Az oldatmátrixnak tartalmaznia kell egy 1-et az első sor első pozíciójában. Ahhoz, hogy a 3-at "1-re változtassuk", megszorozhatjuk a teljes sort 1/3-mal. Ez létrehozza az új R1 értékét: [1,1 / 3, -1 / 3,3].
   • Ügyeljen arra, hogy a negatív jeleket ott hagyja, ahová tartoznak.
3. Használja a sorok összeadását vagy kivonását. A második eszköz, amelyet használhat, hogy a mátrix két sorát hozzáadja vagy kivonja. Ahhoz, hogy a 0 kifejezést létrehozhassa a megoldási mátrixban, számokat kell hozzáadnia vagy kivonnia, hogy elérje a 0-t. Például, ha R1 egy mátrix [1,4,3,2] és R2 [1,3,5,8], akkor kivonhatja az első sort a második sorból, és létrehozhat egy új sort [0, -1, 2.6], mert 1-1 = 0 (első oszlop), 3-4 = -1 (második oszlop), 5-3 = 2 (harmadik oszlop) és 8-2 = 6 (negyedik oszlop). Sor hozzáadás vagy kivonás végrehajtásakor írja át az új eredményt a kezdett sor helyett. Ebben az esetben kivonjuk a 2. sort, és beillesztjük az új sort [0, -1,2,6].
   • Használhat gyorsírási jelölést, és deklarálhatja ezt a műveletet R2-R1 = [0, -1,2,6] értékkel.
   • Ne feledje, hogy az összeadás és a kivonás ugyanannak a műveletnek éppen ellentétes formája. Gondoljon arra, hogy két számot ad hozzá, vagy kivonja az ellenkezőjét. Például, ha a 3-3 = 0 egyszerű egyenlettel indulunk, akkor ezt úgy gondolhatjuk, mint a 3 + (- 3) = 0 összeadási problémát. Az eredmény ugyanaz. Ez egyszerűnek tűnik, de néha könnyebb egy problémát ilyen vagy olyan formában figyelembe venni. Csak figyelje negatív jeleit.
4. Kombinálja a sorok összeadását és a skaláris szorzást egyetlen lépésben. Nem számíthat arra, hogy a kifejezések mindig egyeznek, ezért egyszerű összeadással vagy kivonással 0-kat hozhat létre a mátrixban. Gyakrabban többször kell összeadnia (vagy kivonni) egy másik sorból. Ehhez először meg kell tennie a skaláris szorzást, majd hozzá kell adni azt az eredményt a módosítani kívánt célsorhoz.
   • Tegyük fel; hogy van egy sor [1,1,2,6] és egy második sor [2,3,1,1]. 0 kifejezést szeretne az R2 első oszlopába. Vagyis a 2-t 0-ra akarja változtatni. Ehhez le kell vonnia egy 2-t. Akkor kaphat 2-t, ha először megszorozza az 1. sort a skaláris szorzattal 2, majd kivonja az első sort a második sorból. Rövid formában ez leírható R2-2 * R1 néven. Először szorozd meg R1-et 2-vel, hogy [2,2,4,12] -et kapj. Ezután vonja le ezt R2-ből, hogy [(2-2), (3-2), (1-4), (1-12)] kapjon. Egyszerűsítse ezt, és az új R2 értéke [0,1, -3, -11] lesz.
5. Másolja azokat a sorokat, amelyek változatlanok maradnak munka közben. A mátrixon dolgozva egyszerre csak egy sort fog megváltoztatni, akár skaláris szorzással, sor összeadással vagy sor kivonással, akár lépések kombinációjával. Amikor megváltoztatja az egyik sort, mindenképpen másolja át a mátrix többi sorát az eredeti formájukba.
   • Gyakori hiba lép fel, ha kombinált szorzási és összeadási lépést hajt végre egy lépésben. Tegyük fel például, hogy kétszer kell levonni az R1-et az R2-ből. Amikor ennek a lépésnek a szorzatával R1-et megszorozza 2-vel, ne feledje, hogy R1 nem változik a mátrixban. A szorzást csak az R2 megváltoztatásához hajtja végre. Először másolja az R1-et eredeti formájában, majd változtassa meg az R2-t.
6. Első munka fentről lefelé. A rendszer megoldása érdekében nagyon szervezett mintában dolgozik, lényegében a mátrix egy tagját "megoldja" egyszerre. A háromváltozós tömb szekvenciája így fog kinézni:
   • 1. Készítsen 1-et az első sor első oszlopában (R1C1).
   • 2. Készítsen 0-t a második sor első oszlopában (R2C1).
   • 3. Készítsen 1-et a második sor második oszlopában (R2C2).
   • 4. Készítsen 0-t a harmadik sor első oszlopában (R3C1).
   • 5. Készítsen 0-t a harmadik sor második oszlopában (R3C2).
   • 6. Készítsen 1-et a harmadik sor harmadik oszlopában (R3C3).
7. Dolgozzon vissza alulról felfelé. Ezen a ponton, ha helyesen hajtotta végre a lépéseket, akkor a megoldás felénél jár. Átlós vonalának 1-nek kell lennie, 0-val alatta. A negyedik oszlopban szereplő számok ekkor nem számítanak. Most a következőképpen tér vissza a csúcsra:
   • Hozzon létre egy 0 értéket a második sor harmadik oszlopában (R2C3).
   • Hozzon létre egy 0-t az első sor harmadik oszlopában (R1C3).
   • Hozzon létre egy 0 értéket az első sor második oszlopában (R1C2).
8. Ellenőrizze, hogy létrehozta-e a megoldási mátrixot. Ha a munkája helytálló, akkor létrehozta a megoldási mátrixot úgy, hogy az első három oszlop többi pozíciójában 1-esek legyenek az R1C1, R2C2, R3C3 és 0 átlós vonalában. A negyedik oszlopban szereplő számok jelentik a megoldást az Ön lineáris rendszerére.

4. rész: Összeolvasztja a galaxis megoldásának lépéseit

1. Kezdjük egy lineáris egyenletrendszerrel. E lépések gyakorlásához kezdjük azzal a rendszerrel, amelyet korábban használtunk: 3x + y-z = 9, 2x-2y + z = -3 és x + y + z = 7. Ha ezt mátrixba írja, akkor R1 = [3,1, -1,9], R2 = [2, -2,1, -3] és R3 = [1,1,1,7].
2. Hozzon létre egy 1-et az R1C1 első pozícióban. Vegye figyelembe, hogy az R1 ezen a ponton 3-mal kezdődik, és ezt 1-re kell változtatnia. Ezt megteheti skaláris szorzással, megszorozva az R1 mind a négy tagját 1/3-mal. Gyorsan R1 * 1/3 néven írhat. Ez új eredményt ad R1 esetén, ha R1 = [1,1 / 3, -1 / 3,3]. Másolja az R2-t és az R2-t változatlanul, ha R2 = [2, -2,1, -3] és R3 = [1,1,1,7].
   • Vegye figyelembe, hogy a szorzás és osztás csak inverz függvények egymásnak. Mondhatjuk, hogy az eredmény megváltoztatása nélkül szorozzuk 1/3-mal vagy osztjuk 3-mal.
3. Hozzon létre egy 0-t a második sor első oszlopában (R2C1). Ezen a ponton R2 = [2, -2,1, -3]. Ahhoz, hogy közelebb kerülj a megoldás mátrixához, meg kell változtatnia az első tagot 2-ről 0-ra. Ezt megteheti úgy, hogy kivonja az R1 értékének kétszeresét, mivel R1 1-gyel kezdődik. Röviden: az R2- 2 * művelet * R1. Ne feledje, hogy nem változtatja meg az R1-et, csak dolgozik vele. Tehát először másolja az R1-et, ha R1 = [1,1 / 3, -1 / 3,3]. Majd ha megduplázza az R1 minden tagját, akkor 2 * R1 = [2,2 / 3, -2 / 3,6] lesz. Végül vonja le ezt az eredményt az eredeti R2-ből, hogy megkapja az új R2-t. A kifejezés kifejezésenkénti munkaidő szerint ez a kivonás (2-2), (-2-2 / 3), (1 - (- 2/3)), (-3-6) lesz. Ezeket egyszerűsítjük az új R2 = [0, -8 / 3,5 / 3, -9] értékre. Vegye figyelembe, hogy az első kifejezés 0 (bármi is volt a célja).
   • Írja a 3. sort (amely nem változott) R3 = [1,1,1,7].
   • A negatív számok kivonásával vigyázzon, hogy a jelek helyesek maradjanak.
   • Most először hagyjuk a frakciókat nem megfelelő formájukban. Ez megkönnyíti a megoldás későbbi lépéseit. A feladat utolsó lépésében egyszerűsítheti a törtrészeket.
4. Hozzon létre egy 1-et a második sor második oszlopában (R2C2). Az 1-esek átlós vonalának kialakításához folytonossá kell alakítania a második -8 / 3-as tagot 1-vé. Tegye ezt úgy, hogy megszorozza a teljes sort ennek a számnak a reciprokával (-3/8). Jelképesen ez a lépés R2 * (- 3/8). Az eredményül kapott második sor: R2 = [0,1, -5 / 8,27 / 8].
   • Vegye figyelembe, hogy ha a sor bal fele kezd hasonlítani az oldathoz a 0 és az 1 értékkel, akkor a jobb fele csúnyának tűnhet, nem megfelelő frakciókkal. Csak hagyja őket arra, ami most van.
   • Ne felejtse el folytatni az érintetlen sorok másolását, így R1 = [1,1 / 3, -1 / 3,3] és R3 = [1,1,1,7].
5. Hozzon létre egy 0 értéket a harmadik sor első oszlopában (R3C1). A fókusz most a harmadik sorra kerül, R3 = [1,1,1,7]. Ahhoz, hogy 0 legyen az első pozícióban, ki kell vonni egy 1-et az abban a pillanatban lévő 1-ből. Ha felnéz, van egy 1 az R1 első pozícióján. Tehát csak R1-et kell levonni az R3-ból, hogy megkapja a kívánt eredményt. A kifejezés futamideje (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3). Ez a négy mini probléma egyszerűsíthető az új R3 = [0,2 / 3,4 / 3,4] értékre.
   • Folytassa a másolást R1 = [1.1 / 3, -1 / 3.3] és R2 = [0.1, -5 / 8.27 / 8] mentén. Ne feledje, hogy egyszerre csak egy sort cserél.
6. Készítsen 0-t a harmadik sor második oszlopában (R3C2). Ez az érték jelenleg 2/3, de 0-ra kell konvertálni. Első pillantásra úgy tűnik, hogy duplájával kivonhatja az R1 értékeket, mivel az R1 megfelelő oszlopa 1/3-at tartalmaz. Ha azonban duplázza és kivonja az R1 összes értékét, akkor az R3 első oszlopában szereplő 0 megváltozik, amelyet nem kíván. Ez visszalépés lenne a megoldásában. Tehát az R2 valamilyen kombinációjával kell dolgozni. Ha a 2/3-ot kivonja az R2-ből, a második oszlopban 0 jön létre, az első oszlop megváltoztatása nélkül. Röviden: ez R3-2 / 3 * R2. Az egyes kifejezések: (0-0), (2 / 3-2 / 3), (4/3 - (- - 5/3 * 2/3)), (4-27 / 8 * 2/3) . Az egyszerűsítés ekkor R3 = [0,0,42 / 24,42 / 24].
7. Hozzon létre egy 1-et a harmadik sor harmadik oszlopában (R3C3). Ez egy egyszerű szorzás a szám reciprokával, amit mond. A jelenlegi érték 42/24, tehát 24/42-vel szorozva megkapja a kívánt értéket 1. Megjegyezzük, hogy az első két kifejezés egyaránt 0, így minden szorzás 0 marad. Az R3 új értéke = [0,0,1,1].
   • Ne feledje, hogy az előző lépésben meglehetősen bonyolultnak tűnő frakciók már kezdenek oldódni.
   • Folytassa R1 = [1.1 / 3, -1 / 3.3] és R2 = [0.1, -5 / 8.27 / 8] értékkel.
   • Vegye figyelembe, hogy ezen a ponton az 1-es átlója van az oldatmátrixának. A megoldás megtalálásához csak a mátrix három elemét kell átalakítania 0-ra.
8. Hozzon létre egy 0 értéket a második sor harmadik oszlopában. R2 jelenleg [0,1, -5 / 8,27 / 8], értéke a harmadik oszlopban -5 / 8. Ezt 0-val kell átalakítania. Ez azt jelenti, hogy el kell végeznie valamilyen műveletet az R3-mal, amely 5/8 hozzáadásából áll. Mivel az R3 megfelelő harmadik oszlopa 1, az R3 összes értékét meg kell szorozni 5/8-mal, és az eredményt hozzá kell adni az R2-hez. Röviden ez R2 + 5/8 * R3. A kifejezés kifejezés R2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8). Ez egyszerűsíthető R2 = [0,1,0,4] -re.
   • Ezután másolja R1 = [1,1 / 3, -1 / 3,3] és R3 = [0,0,1,1].
9. Hozzon létre egy 0 értéket az első sor harmadik oszlopában (R1C3). Az első sor jelenleg R1 = [1,1 / 3, -1 / 3,3]. A harmadik oszlopban szereplő -1/3 értéket 0-ra kell konvertálni, az R3 valamilyen kombinációjával. Nem akarja használni az R2-t, mert az R2 második oszlopában szereplő 1 rosszul változtatná meg az R1-et. Tehát megszorozzuk az R3 * 1/3 értéket, és az eredményt hozzáadjuk az R1 értékhez. Ennek jelölése R1 + 1/3 * R3. A kifejezés kidolgozásának kifejezése R1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3). Ezt egyszerűsítheti új R1 = [1,1 / 3,0,10 / 3] értékre.
   • Másolja a változatlan R2 = [0,1,0,4] és R3 = [0,0,1,1] értékeket.
10. Készítsen 0-t az első sor második oszlopában (R1C2). Ha mindent helyesen végeznek, akkor ez legyen az utolsó lépés. A második oszlopban szereplő 1/3-át 0-ra kell konvertálni. Ezt úgy kaphatja meg, hogy megszorozza és kivonja az R2 * 1/3 értéket. Röviden, ez R1-1 / 3 * R2. Az eredmény R1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3). Az egyszerűsítés ekkor R1 = [1,0,0,2].
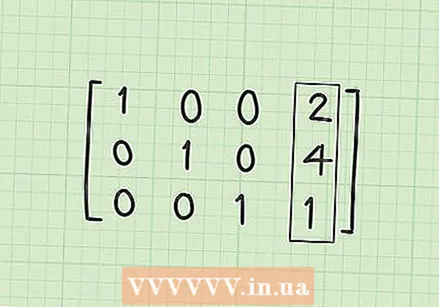11. Keresse meg a megoldási mátrixot. Ezen a ponton, ha minden jól megy, akkor a három sor R1 = [1,0,0,2], R2 = [0,1,0,4] és R3 = [0,0,1,1] lennie kell. Ne feledje, hogy ha ezt a blokkmátrix űrlapba úgy írja be, hogy a sorok egymás fölé kerülnek, akkor az 1-es átlósok vannak a 0-val tovább, és a megoldások a negyedik oszlopban vannak. A megoldásmátrixnak így kell kinéznie:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. Megértése a megoldás. Miután a lineáris egyenleteket mátrixsá konvertálta, az x együtthatókat az első oszlopba, az y együtthatókat a második oszlopba, a z együtthatókat a harmadik oszlopokba teszi. Ha újra át akarja írni a mátrixot egyenletekre, akkor a mátrix ezen három vonala valójában a három egyenletet jelenti: 1x + 0y + 0z = 2, 0x + 1y + 0z = 4, és 0x + 0y + 1z = 1. Mivel áthúzhatjuk a 0 tagot, és nem kell megírnunk az 1 együtthatót, ez a három egyenlet egyszerűsíti a megoldást: x = 2, y = 4 és z = 1. Ez a megoldás a lineáris egyenletrendszerére.

4/4 rész: A megoldás ellenőrzése

1. Az egyenlet minden változójába foglalja bele a megoldásokat. Mindig célszerű ellenőrizni, hogy a megoldás valóban helyes-e. Ezt úgy teszi meg, hogy teszteli az eredményeket az eredeti egyenletekben.
   • E probléma eredeti egyenletei a következők voltak: 3x + y-z = 9, 2x-2y + z = -3 és x + y + z = 7. Ha a változókat lecseréli a talált értékekre, akkor 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3 és 2 + 4 + 1 = 7 értéket kap.
2. Egyszerűsítsen minden összehasonlítást. Végezze el az egyes egyenletek műveleteit a műveletek alapszabályainak megfelelően. Az első egyenlet 6 + 4-1 = 9-re vagy 9 = 9-re egyszerűsödik. A második egyenlet egyszerűsíthető 4-8 + 1 = -3-ra vagy -3 = -3-ra. Az utolsó egyenlet egyszerűen 7 = 7.
   • Mivel bármely egyenlet valódi matematikai állítássá egyszerűsödik, a megoldások helyesek. Ha bármelyik megoldás helytelen, ellenőrizze újra a munkáját, és keresse meg az esetleges hibákat. Néhány általános hiba akkor fordul elő, amikor útközben megszabadulunk a mínuszjelektől, vagy összekeverjük a törtek szorzását és összeadását.
3. Írja ki a végső megoldásait. Erre az adott feladatra a végső megoldás x = 2, y = 4 és z = 1.

Tippek

• Ha az egyenletrendszere nagyon összetett, sok változóval rendelkezik, akkor használhatja a grafikus számológépet ahelyett, hogy kézzel végezné a munkát. Erről további információt a wikiHow webhelyen talál.