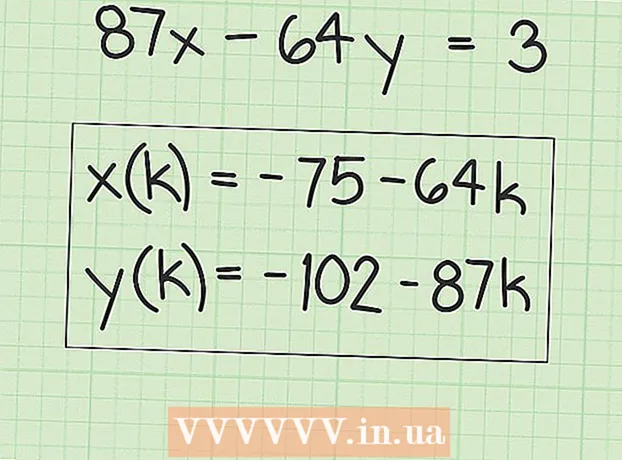
Tartalom

• Lépések
• Rész 1 /4: Hogyan írjunk egyenletet?
• 2. rész a 4 -ből: Hogyan írjuk meg Euklidész algoritmusát
• 3. rész a 4 -ből: Hogyan lehet megoldást találni Euklidész algoritmusa segítségével?
• 4. rész a 4 -ből: Keressen végtelen más megoldásokat

Egy lineáris Diophantine egyenlet megoldásához meg kell találnia az "x" és "y" változók értékeit, amelyek egész számok. Egy egész számú megoldás a szokásosnál összetettebb, és meghatározott műveletsort igényel. Először ki kell számítani az együtthatók legnagyobb közös osztóját (GCD), majd megoldást kell találni. Ha talált egy egész megoldást egy lineáris egyenletre, akkor egy egyszerű minta segítségével végtelen számú más megoldást találhat.

Lépések

Rész 1 /4: Hogyan írjunk egyenletet?

1. 1 Írja le az egyenletet szabványos formában. A lineáris egyenlet olyan egyenlet, amelyben a változók kitevői nem haladják meg az 1 -et. Egy ilyen lineáris egyenlet megoldásához először írja fel szabványos formában. A lineáris egyenlet standard formája így néz ki: ${ displaystyle Ax + By = C}$, ahol ${ displaystyle A, B}$ és ${ displaystyle C}$ - egész számok.
   • Ha az egyenletet más formában adjuk meg, hozzuk szabványos formába az alapvető algebrai műveletek segítségével. Például, ha megadjuk az egyenletet ${ displaystyle 23x + 4y -7x = -3y + 15}$... Adjon meg hasonló kifejezéseket, és írja le az egyenletet: ${ displaystyle 16x + 7y = 15}$.
2. 2 Egyszerűsítse az egyenletet (ha lehetséges). Ha szabványos formában írja be az egyenletet, nézze meg az együtthatókat ${ displaystyle A, B}$ és ${ displaystyle C}$... Ha ezeknek az esélyeknek GCD -je van, ossza el mindhárom szorzót ezzel. Az ilyen egyszerűsített egyenlet megoldása az eredeti egyenlet megoldása is lesz.
   • Például, ha mindhárom együttható páros, ossza meg őket legalább 2 -vel. Például:
     • ${ displaystyle 42x + 36y = 48}$ (minden tag osztható 2 -vel)
     • ${ displaystyle 21x + 18y = 24}$ (most minden tag osztható 3 -mal)
     • ${ displaystyle 7x + 6y = 8}$ (ez az egyenlet már nem egyszerűsíthető)
3. 3 Ellenőrizze, hogy az egyenlet megoldható -e. Bizonyos esetekben azonnal kijelentheti, hogy az egyenletnek nincs megoldása. Ha a "C" együttható nem osztható az "A" és a "B" együttható GCD -jével, akkor az egyenletnek nincs megoldása.
   • Például, ha mindkét együttható ${ displaystyle A}$ és ${ displaystyle B}$ párosak, akkor az együttható ${ displaystyle C}$ egyenletesnek kell lennie. De ha ${ displaystyle C}$ furcsa, akkor nincs megoldás.
     • Az egyenlet ${ displaystyle 2x + 4y = 21}$ nincs egész megoldás.
     • Az egyenlet ${ displaystyle 5x + 10y = 17}$ nincs egész megoldás, mivel az egyenlet bal oldala osztható 5 -tel, a jobb pedig nem.

2. rész a 4 -ből: Hogyan írjuk meg Euklidész algoritmusát

1. 1 Ismerje meg Euklidész algoritmusát. Ez ismétlődő osztások sorozata, amelyben az előző maradékot használják fel következő osztóként. Az utolsó osztó, amely a számokat integrálisan osztja, a két szám legnagyobb közös osztója (GCD).
   • Például keressük meg a 272 és 36 számok GCD -jét Euklidész algoritmusával:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Ossza el a nagyobb számot (272) a kicsivel (36), és figyeljen a maradékra (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - ossza el az előző osztót (36) az előző maradékkal (20). Jegyezze fel az új maradékot (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - ossza el az előző osztót (20) az előző maradékkal (16). Jegyezze fel az új maradékot (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Ossza el az előző osztót (16) az előző maradékkal (4). Mivel a maradék 0, azt mondhatjuk, hogy 4 az eredeti két 272 és 36 szám GCD -je.
2. 2 Alkalmazza Euklidész algoritmusát az "A" és a "B" együtthatóra. Amikor a lineáris egyenletet szabványos formában írja, határozza meg az "A" és a "B" együtthatót, majd alkalmazza rájuk Euklidész algoritmusát a GCD megkereséséhez. Például adott egy lineáris egyenlet ${ displaystyle 87x-64y = 3}$.
   • Itt van Euclid algoritmusa az A = 87 és B = 64 együtthatókra:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Keresse meg a legnagyobb közös tényezőt (GCD). Mivel az utolsó osztó 1 volt, a GCD 87 és 64 az 1. Így a 87 és 64 prímszám egymáshoz képest.
4. 4 Elemezze az eredményt. Amikor megtalálja a gcd együtthatókat ${ displaystyle A}$ és ${ displaystyle B}$, hasonlítsa össze az együtthatóval ${ displaystyle C}$ az eredeti egyenlet. Ha ${ displaystyle C}$ osztható gcd -vel ${ displaystyle A}$ és ${ displaystyle B}$, az egyenletnek egész megoldása van; különben az egyenletnek nincs megoldása.
   • Például az egyenlet ${ displaystyle 87x-64y = 3}$ megoldható, mert 3 osztható 1 -gyel (gcd = 1).
   • Tegyük fel például, hogy GCD = 5. A 3 nem osztható egyenletesen 5 -tel, így ennek az egyenletnek nincs egész megoldása.
   • Amint az alábbiakban látható, ha egy egyenletnek egy egész számú megoldása van, akkor végtelen számú más egész megoldást is tartalmaz.

3. rész a 4 -ből: Hogyan lehet megoldást találni Euklidész algoritmusa segítségével?

1. 1 Számozza meg a GCD kiszámításának lépéseit. A lineáris egyenlet megoldásának megtalálásához az euklideszi algoritmust kell használnia a helyettesítési és egyszerűsítési folyamat alapjául.
   • Kezdje a GCD kiszámításának lépéseinek számozásával. A számítási folyamat így néz ki:
     • ${ displaystyle { text {1. lépés}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {2. lépés}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {3. lépés}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {4. lépés}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {5. lépés}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {6. lépés}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {7. lépés}}: 2 = (2 * 1) +0}$
2. 2 Ügyeljen az utolsó lépésre, ahol maradék van. Írja át ennek a lépésnek az egyenletét a maradék izolálásához.
   • Példánkban az utolsó lépés a maradékkal a 6. lépés. A maradék 1. Írja át az egyenletet a 6. lépésben az alábbiak szerint:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Izolálja az előző lépés többi részét. Ez a folyamat lépésről lépésre "felfelé". Minden alkalommal, amikor elkülöníti a fennmaradó részt az előző lépés egyenletében.
   • Izolálja az egyenlet fennmaradó részét az 5. lépésben:
     • ${ displaystyle 2 = 5- (1 * 3)}$ vagy ${ displaystyle 2 = 5-3}$
4. 4 Helyettesítse és egyszerűsítse. Figyeljük meg, hogy a 6. lépésben szereplő egyenlet a 2 -es számot tartalmazza, az 5. lépésben pedig a 2 -es számot izoláljuk. Tehát a „2” helyett a 6. lépés egyenletében helyettesítse az 5. lépésben szereplő kifejezést:
   • ${ displaystyle 1 = 3-2}$ (a 6. lépés egyenlete)
   • ${ displaystyle 1 = 3- (5-3)}$ (2 helyett egy kifejezést helyettesítettek)
   • ${ displaystyle 1 = 3-5 + 3}$ (nyitott zárójelek)
   • ${ displaystyle 1 = 2 (3) -5}$ (egyszerűsített)
5. 5 Ismételje meg a helyettesítési és egyszerűsítési folyamatot. Ismételje meg a leírt folyamatot, fordított sorrendben haladva az euklideszi algoritmuson. Minden alkalommal, amikor újraírja az egyenletet az előző lépésből, és bedugja az utolsó kapott egyenletbe.
   • Az utolsó lépés, amelyet megvizsgáltunk, az 5. lépés volt. Tehát folytassa a 4. lépéssel, és izolálja a maradékot az adott lépés egyenletében:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Helyettesítse ezt a kifejezést a "3" kifejezéssel az utolsó egyenletben:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Folytassa a helyettesítési és egyszerűsítési folyamatot. Ezt a folyamatot addig kell ismételni, amíg el nem éri az euklideszi algoritmus kezdeti lépését. A folyamat célja az egyenlet felírása a megoldandó eredeti egyenlet 87 és 64 együtthatóival. Példánkban:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (helyettesítette a 3. lépésben szereplő kifejezést)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (helyettesítette a 2. lépésben szereplő kifejezést)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (helyettesítette az 1. lépésben szereplő kifejezést)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Írja át a kapott egyenletet az eredeti együtthatóknak megfelelően. Amikor visszatér az euklideszi algoritmus első lépéséhez, látni fogja, hogy a kapott egyenlet az eredeti egyenlet két együtthatóját tartalmazza. Írja át az egyenletet úgy, hogy tagjai sorrendje megfeleljen az eredeti egyenlet együtthatóinak.
   • Példánkban az eredeti egyenlet ${ displaystyle 87x-64y = 3}$... Ezért írja át a kapott egyenletet úgy, hogy az együtthatók összhangban legyenek.Különös figyelmet kell fordítani a "64" együtthatóra. Az eredeti egyenletben ez az együttható negatív, az euklideszi algoritmusban pedig pozitív. Ezért a 34 -es tényezőt negatívvá kell tenni. A végső egyenletet így írjuk le:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Alkalmazza a megfelelő szorzót a megoldás megtalálásához. Vegye figyelembe, hogy példánkban GCD = 1, tehát a végső egyenlet 1. De az eredeti (87x-64y) egyenlet 3. Ezért a végső egyenlet összes tagját meg kell szorozni 3-mal a megoldás érdekében:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Írja le az egész megoldást az egyenlethez. Az eredeti egyenlet együtthatóival megszorzott számok jelentik az egyenlet megoldásait.
   • Példánkban írja be a megoldást koordinátapárként: ${ displaystyle (x, y) = ( - 75, -102)}$.

4. rész a 4 -ből: Keressen végtelen más megoldásokat

1. 1 Értsd meg, hogy végtelen számú megoldás létezik. Ha egy lineáris egyenletnek egy egész számú megoldása van, akkor végtelen sok egész megoldást kell tartalmaznia. Íme egy gyors bizonyítás (algebrai formában):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (ha hozzáadja a "B" betűt az "x" -hez, és kivonja az "A" -t az "y" -ből, akkor az eredeti egyenlet értéke nem változik)
2. 2 Jegyezze fel az eredeti x és y értékeket. A következő (végtelen) megoldások kiszámításához használt sablon az egyetlen megoldással kezdődik, amelyet már talált.
   • Példánkban a megoldás egy pár koordináta ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 Adja hozzá a "B" tényezőt az "x" értékhez. Ezzel keresse meg az új x értéket.
   • Példánkban x = -75 és B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • Így az új "x" érték: x = -139.
4. 4 Vonja le az "A" tényezőt az "y" értékből. Annak érdekében, hogy az eredeti egyenlet értéke ne változzon, amikor egy számot hozzáad az "x" -hez, ki kell vonnia egy másik számot az "y" -ből.
   • Példánkban y = -102 és A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Így az "y" új értéke: y = -189.
   • Az új koordinátapár így lesz írva: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Ellenőrizze a megoldást. Annak ellenőrzéséhez, hogy az új koordinátapár megoldás az eredeti egyenletre, csatlakoztassa az értékeket az egyenlethez.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Mivel az egyenlőség teljesül, a döntés helyes.
6. 6 Írjon le kifejezéseket, hogy sok megoldást találjon. Az "x" érték megegyezik az eredeti megoldással és a "B" tényező tetszőleges többszörösével. Ezt a következő kifejezéssel lehet leírni:
   • x (k) = x + k (B), ahol az „x (k)” az „x” értékek halmaza, és az „x” az Ön által talált „x” eredeti (első) értéke.
     • Példánkban:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), ahol y (k) az y értékek halmaza, és y az eredeti (első) y érték, amelyet talált.
     • Példánkban:
     • ${ displaystyle y (k) = - 102-87k}$