Tartalom

• Lépések
• Tanács

A sebességet úgy definiáljuk, mint egy objektum adott irányú sebességét. Sok esetben a sebesség megtalálásához a v = s / t egyenletet fogjuk használni, ahol v a sebesség, s az objektum elmozdulásának teljes távolsága az eredeti helyzettől, és t az az idő, amelybe a tárgy halad. menj végig az egész úton. Elméletileg azonban ez a képlet csak a sebességre vonatkozik közepes dolgok útközben. Az objektum sebességének kiszámításával az adott pillanatban a távolság mentén. Vagyis Szállítási idő és az egyenlet határozza meg v = (ds) / (dt), vagy más szavakkal, az átlagsebesség egyenletének a deriváltja.

Lépések

1/3 rész: Számítsa ki a pillanatnyi sebességet

1. 

   
   
   Kezdje egy egyenlettel a sebesség elmozdulási távolság alapján történő kiszámításához. A pillanatnyi sebesség megtalálásához először rendelkeznünk kell egy olyan egyenlettel, amely az adott objektum helyzetét (elmozdulást tekintve) az adott időpontban jelzi. Ez azt jelenti, hogy az egyenletnek csak egy változója lehet S egyik oldalon és forduljon meg t A másik oldalon (nem feltétlenül csak egy változó), így:
   

   s = -1,5t + 10t + 4

   • Ebben az egyenletben a változók a következők:

     s = elmozdulás. A tárgy távolsága az eredeti helyzetétől. Például, ha egy tárgy 10 métert előre és 7 métert hátra tud járni, akkor annak teljes távolsága 10 - 7 = 3 méter (nem 10 + 7 = 17m).

     t = idő. Ez a változó magyarázat nélkül egyszerű, általában másodpercekben mérve.

2. 

   
   
   Vegyük az egyenlet deriváltját. Az egyenlet deriváltja egy másik egyenlet, amely a távolság meredekségét mutatja egy adott időpontban. Az egyenlet származtatási távolság szerinti deriváltjának megtalálásához vegye fel a függvény differenciálját a következő általános szabály szerint a derivált kiszámításához: Ha y = a * x, akkor Származék = a * n * x. Ez vonatkozik az egyenlet "t" oldalán lévő összes kifejezésre.
   • Más szavakkal, kezdje el kapni a differenciál balról jobbra az egyenlet "t" oldalán. Valahányszor találkozik a "t" változóval, kivonja a kitevőt 1-gyel, és megszorozza a kifejezést az eredeti kitevővel. Minden állandó kifejezés („t” nélküli kifejezés) eltűnik, mert szorozzuk 0-val. A folyamat valójában nem olyan nehéz, mint gondolnánk - vegyük példának a fenti lépésben szereplő egyenletet:
     

     s = -1,5t + 10t + 4
     (2) -1,5t + (1) 10t + (0) 4t
     -3t + 10t
     -3t + 10

     
     

3. 

   Cserélje az "s" szót a "ds / dt" kifejezésre. Annak bemutatására, hogy az új egyenlet az eredeti négyzet deriváltja, az "s" -t "ds / dt" szimbólummal helyettesítjük. Elméletileg ez a jelölés "s deriváltja t szempontjából". A jelölés megértésének egyszerűbb módja: ds / dt a kezdeti egyenlet bármely pontjának meredeksége. Például, hogy megtaláljuk az s = -1,5t + 10t + 4 egyenlet által leírt távolság meredekségét a t = 5 időpontban, t helyettesítjük az "5" -t az egyenlet deriváltjában.
   • A fenti példában az egyenlet deriváltja így néz ki:
     

     ds / dt = -3t + 10

4. 

   Helyettesítsen egy t értéket az új egyenletbe a pillanatnyi sebesség megállapításához. Most, hogy megvan a derivált egyenlet, nagyon egyszerű megtalálni a pillanatnyi sebességet az adott pillanatban. Csak annyit kell tennie, hogy kiválaszt egy t-értéket, és lecseréli a derivált egyenletre. Például, ha meg akarjuk találni a pillanatnyi sebességet t = 5-nél, akkor a ds / dt = -3t + 10 deriváltegyenletben t-vel "5" -t kell kicserélnünk. Az egyenletet így oldjuk meg:
   

   ds / dt = -3t + 10
   ds / dt = -3 (5) + 10
   ds / dt = -15 + 10 = -5 méter / másodperc

   • Vegye figyelembe, hogy a fenti "méter / másodperc" mértékegységet használjuk.Mivel a problémát az elmozdulás méterben és az idő másodpercben megoldjuk, és a sebesség az elmozdulás időben, ez az egység alkalmas.
   hirdetés

2. rész: 3: A pillanatnyi sebesség grafikus becslése

1. 

   Ábrázolja az objektum időbeli mozgási távolságát. A fenti szakaszban azt mondtuk, hogy a derivált egy olyan képlet is, amely lehetővé teszi számunkra, hogy megtaláljuk a meredekséget a deriváltból vett egyenlet bármely pontján. Valójában, ha az objektum mozgási távolságát ábrázolja egy grafikonon, A gráf meredeksége bármely pontban az objektum pillanatnyi sebessége abban a pontban.
   • A mozgási távolságok ábrázolásához használja az x tengelyt az idő, az y tengelyt pedig az elmozduláshoz. Ezután meghatároz egy pontszámot a t értékeinek a mozgásegyenletbe való bedugásával, az eredmény s érték, és a t, s (x, y) pontokat pontozza a grafikonon.
   • Vegye figyelembe, hogy a grafikon az x tengely alá nyúlhat. Ha az objektum mozgását mutató vonal lefelé halad az x tengelyen, ez azt jelenti, hogy az objektum az eredeti helyzetéből visszafelé mozog. Általánosságban elmondható, hogy a grafikon nem fog kinyúlni az y tengely mögé - általában nem mérjük az időben visszafelé haladó tárgyak sebességét!

2. 

   Válasszon egy P pontot és egy Q pontot, amely a P pont közelében helyezkedik el a grafikonon. A grafikon meredekségének megtalálásához a P pontban a "határkeresés" technikáját alkalmazzuk. Határ megtalálása azt jelenti, hogy két pontot (P és Q (P közelében lévő pont)) veszünk fel a görbén, és megtaláljuk a két pontot összekötő egyenes meredekségét, ismételve ezt a folyamatot, amikor a P és Q távolsága rövidül. fokozatosan.
   • Tegyük fel, hogy az elmozdulási távolságnak vannak pontjai (1; 3) és (4; 7). Ebben az esetben, ha meg akarjuk találni a lejtést az (1; 3) pontnál, akkor beállíthatjuk (1; 3) = P és (4; 7) = Q.

3. 

   Keresse meg a lejtést P és Q között. A P és Q közötti meredekség a P és Q y értékek különbsége a P és Q x értékeinek különbségétől. Más szavakkal, H = (y_Q - y_P) / (x_Q - x_P), ahol H a két pont közötti meredekség. Ebben a példában a P és Q közötti meredekség:
   

   H = (y_Q - y_P) / (x_Q - x_P)
   H = (7 - 3) / (4 - 1)
   H = (4) / (3) = 1,33

4. 

   Ismételje meg többször úgy, hogy Q-t közelebb helyezi P-hez. A cél a P és Q közötti távolság leszűkítése, amíg el nem érnek egyetlen pontot. Minél kisebb a távolság P és Q között, annál közelebb lesz a végtelenül kicsi szakasz meredeksége a P pont meredekségéhez. Ismételje meg néhányszor a példaegyenletünket a (2; 4 , 8), (1,5; 3,95) és (1,25; 3,49) Q-t ad, és P kezdeti koordinátái: (1; 3):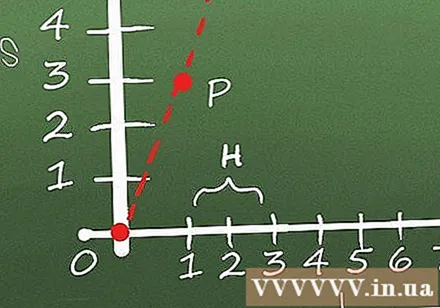
   

   Q = (2; 4,8): H = (4,8 - 3) / (2 - 1)
   H = (1,8) / (1) = 1,8
   
   Q = (1,5; 3,95): H = (3,95 - 3) / (1,5 - 1)
   H = (0,95) / (0,5) = 1,9
   
   Q = (1,25; 3,49): H = (3,49 - 3) / (1,25 - 1)
   H = (0,49) / (0,25) = 1,96

5. 

   Becsüli meg a rendkívül kicsi szakasz meredekségét a gráf görbén. Ahogy Q egyre közelebb kerül P-hez, H fokozatosan közelebb kerül a P-i lejtőhöz. Végül egy nagyon kis vonalnál H lesz a lejtő P-nél. Mivel nem tudunk mérni vagy kiszámítani Egy vonal hossza rendkívül kicsi, ezért csak akkor becsülje meg a meredekséget P-nél, ha az jól látható az általunk kiszámított pontokból.
   • A fenti példában, amikor H-t közelítjük P-hez, a H értéke 1,8; 1,9 és 1,96. Mivel ezek a számok egyre közelebb kerülnek a 2-hez, elmondhatjuk 2 a P lejtés hozzávetőleges értéke
   • Ne feledje, hogy a gráf bármely pontján a meredekség az adott ponton a gráfegyenlet deriváltja. Mivel a grafikon egy objektum időbeli elmozdulását ábrázolja, amint azt az előző szakaszban láttuk, pillanatnyi sebessége bármely pontban az objektum elmozdulási távolságának a derékszáma a problémapontban. Hozzáférés, mondhatjuk 2 méter / sec a pillanatnyi sebesség hozzávetőleges becslése, amikor t = 1.
   hirdetés

3. rész 3: Minta probléma

1. 

   Keresse meg a pillanatnyi sebességet, amikor t = 1 az s = 5t - 3t + 2t + 9 elmozdulási egyenlettel. Mint az első szakaszban szereplő példa, de ez négyzet helyett köbös, tehát ugyanúgy meg tudjuk oldani a problémát.
   • Először vegye fel az egyenlet deriváltját:
     

     s = 5t - 3t + 2t + 9
     s = (3) 5t - (2) 3t + (1) 2t
     15t - 6t + 2t - 6t + 2

   • Ezután helyettesítjük a t (4) értékét:
     

     s = 15t - 6t + 2
     15(4) - 6(4) + 2
     15(16) - 6(4) + 2
     240 - 24 + 2 = 22 méter másodpercenként

2. 

   A grafikonbecslési módszer segítségével keresse meg a pillanatnyi sebességet (1; 3) az s = 4t - t elmozdulási egyenletnél. Ehhez a problémához az (1; 3) koordinátákat használjuk P pontként, de meg kell találnunk a közelében lévő többi Q pontot. Ezután már csak meg kell találnunk a H értékeket és levezetni a becsült értéket.
   • Először Q pontokat találunk, amikor t = 2; 1,5; 1.1 és 1.01.
     

     s = 4t - t
     
     t = 2: s = 4 (2) - (2)
     4 (4) - 2 = 16 - 2 = 14, tehát Q = (2; 14)
     
     t = 1,5: s = 4 (1,5) - (1,5)
     4 (2,25) - 1,5 = 9 - 1,5 = 7,5, tehát Q = (1,5; 7,5)
     
     t = 1,1: s = 4 (1,1) - (1,1)
     4 (1,21) - 1,1 = 4,84 - 1,1 = 3,74, tehát Q = (1,1; 3,74)
     
     t = 1,01: s = 4 (1,01) - (1,01)
     4 (1,0201) - 1,01 = 4,0804 - 1,01 = 3,0704, tehát ennyi Q = (1,01; 3,0704)

   • Ezután H értékeket kapunk:
     

     Q = (2; 14): H = (14 - 3) / (2 - 1)
     H = (11) / (1) = 11
     
     Q = (1,5; 7,5): H = (7,5 - 3) / (1,5 - 1)
     H = (4,5) / (0,5) = 9
     
     Q = (1,1; 3,74): H = (3,74 - 3) / (1,1 - 1)
     H = (0,74) / (0,1) = 7,3
     
     Q = (1,01; 3,0704): H = (3,0704-3) / (1,01-1)
     H = (0,0704) / (0,01) = 7,04

   • Mivel úgy tűnik, hogy a H értékek közelebb vannak a 7-hez, ezt mondhatjuk 7 méter másodpercenként a pillanatnyi sebesség hozzávetőleges becslése a koordinátán (1; 3).
   hirdetés

Tanács

• A gyorsulás (a sebesség változásának időbeli változásának) megkereséséhez használja az első részben alkalmazott módszert az elmozdulási egyenlet deriváltjának megszerzéséhez. Ezután vegye újra a deriváltat az imént talált deriváltegyenlethez. Ennek eredményeként megvan a gyorsulás egyenlete egy adott időpontban - csak annyit kell tennie, hogy bedugja az időt.
• Az Y (elmozdulási távolság) és X (idő) kapcsolatát bemutató egyenlet nagyon egyszerű lehet, például Y = 6x + 3. Ebben az esetben a meredekség állandó, és nem szükséges megtenni a meredekség kiszámításához használt derivált, vagyis egy lineáris gráf Y = mx + b alapegyenlet formáját követi, azaz a meredekség 6.
• Az elmozdulási távolság olyan, mint a távolság, de van iránya, tehát vektormennyiség, a sebesség pedig skaláris mennyiség. Az utazási távolságok negatívak lehetnek, míg a távolságok csak pozitívak lehetnek.