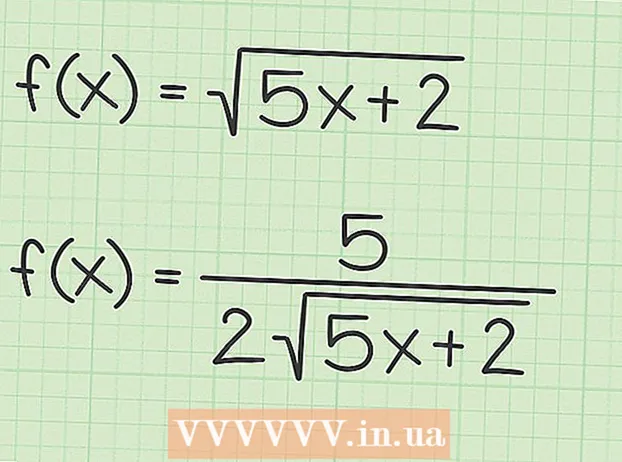
Ha matematikát tanult az iskolában, akkor kétségtelenül megtanulta a hatalom szabályát az egyszerű függvények származékának meghatározásához. Ha azonban a függvény négyzetgyököt vagy négyzetgyököt tartalmaz, például 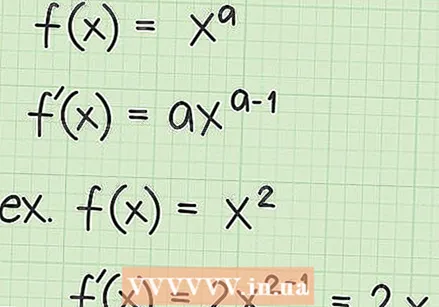${ displaystyle { sqrt {x}}}$Tekintse át a derivatívák teljesítményszabályát. Az első szabály, amelyet valószínűleg megtanultál a származékok megtalálásához, a hatalmi szabály. Ez a sor azt mondja, hogy egy változóra ${ displaystyle x}$Írja át a négyzetgyöket hatványként. A négyzetgyök függvény származékának megtalálásához ne feledje, hogy egy szám vagy változó négyzetgyöke kitevõként is írható. A gyökérjel alatti kifejezést alapként írjuk, az 1/2 erejéig emeljük. A kifejezést a négyzetgyök kitevőjeként is használják. Vessen egy pillantást a következő példákra:

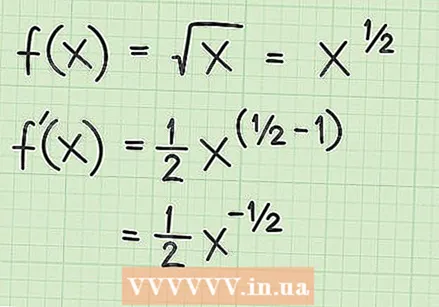• ${ displaystyle { sqrt {x}} = x ^ { frac {1} {2}}}$Alkalmazza a teljesítmény szabályt. Ha a függvény a legegyszerűbb négyzetgyök, 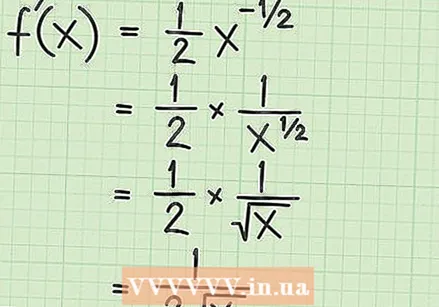${ displaystyle f (x) = { sqrt {x}}}$Egyszerűsítse az eredményt. Ebben a szakaszban tudnia kell, hogy a negatív kitevő azt jelenti, hogy a pozitív hatvány inverzét vesszük, ami a szám lenne. Kitevője 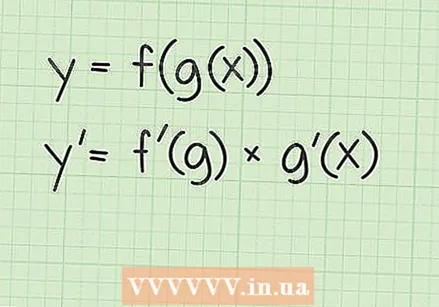${ displaystyle - { frac {1} {2}}}$Tekintse át a láncszabályt a funkciók tekintetében. A láncszabály olyan származtatott szabályok, amelyeket akkor használ, ha az eredeti függvény egy funkciót egy másik függvényben kombinál. A láncszabály ezt két funkcióra mondja ${ displaystyle f (x)}$Határozza meg a láncszabály függvényeit. A láncszabály használatához először meg kell határoznia a kombinált függvényt alkotó két függvényt. 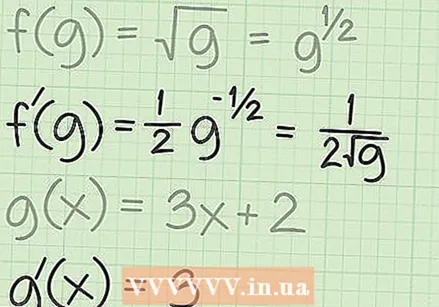Négyzetgyökös függvények esetén a külső függvény ${ displaystyle f (g)}$Meghatározza a két függvény deriváltjait. A láncszabálynak a függvény négyzetgyökére való alkalmazásához először meg kell találnia az általános négyzetgyök függvény származékát:
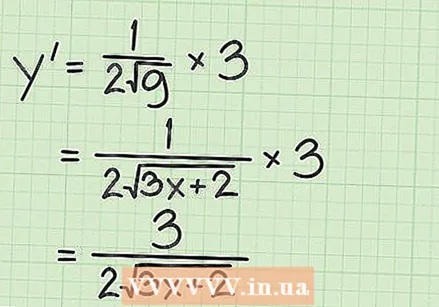  • ${ displaystyle f (g) = { sqrt {g}} = g ^ { frac {1} {2}}}$Kombinálja a függvényeket a láncszabályban. A láncszabály az ${ displaystyle y ^ { prime} = f ^ { prime} (g) * g ^ { prime} (x)}$Határozza meg egy gyökérfüggvény deriváltjait gyors módszerrel. Ha meg akarja találni egy változó vagy egy függvény négyzetgyökének deriváltját, alkalmazhat egy egyszerű szabályt: a derivált mindig a négyzetgyök alatti szám deriváltja lesz, elosztva az eredeti négyzetgyök duplájával. Jelképesen ez a következőképpen ábrázolható:
    • Ha ${ displaystyle f (x) = { sqrt {u}}}$Keresse meg a szám deriváltját a négyzetgyök alatt. Ez egy szám vagy függvény a négyzetgyök előjel alatt. A gyors módszer használatához csak a négyzetgyök alá tartozó szám származékát keresse meg. Tekintsük a következő példákat:
      • A helyzetben ${ displaystyle { sqrt {5x + 2}}}$Írja fel a négyzetgyök szám deriváltját egy tört számlálójaként! A gyökfüggvény deriváltja tartalmazni fog egy töredéket. Ennek a frakciónak a számlálója a négyzetgyök szám deriváltja. Tehát a fenti példafüggvényekben a derivált első része így fog menni:
        • Ha 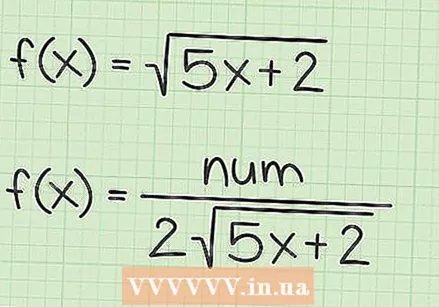${ displaystyle f (x) = { sqrt {5x + 2}}}$Írja a nevezőt az eredeti négyzetgyök duplájára. Ezzel a gyors módszerrel a nevező az eredeti négyzetgyök függvény kétszerese. Tehát a fenti három példafüggvényben a származékok nevezői a következők:
          • Ha ${ displaystyle f (x) = { sqrt {5x + 2}}}$Kombinálja a számlálót és a nevezőt, hogy megtalálja a származékot. Tedd össze a frakció két felét, és az eredmény az eredeti függvény deriváltja lesz.
            • Ha ${ displaystyle f (x) = { sqrt {5x + 2}}}$, mint ${ displaystyle f ^ { prime} (x) = { frac {5} {2 { sqrt {5x + 2}}}}}$
            • Ha ${ displaystyle f (x) = { sqrt {3x ^ {4}}}}$, mint ${ displaystyle f ^ { prime} (x) = { frac {12x ^ {3}} {2 { sqrt {3x ^ {4}}}}}}$
            • Ha ${ displaystyle f (x) = { sqrt { sin (x)}}}$, mint ${ displaystyle f ^ { prime} (x) = { frac { cos (x)} {2 { sqrt { sin (x)}}}}}$