Tartalom

• Lépni
• 1. módszer a 7-ből: Kocka
• 2. módszer a 7-ből: Téglalap alakú prizma
• 3. módszer a 7-ből: Háromszög alakú prizma
• 4/7 módszer: Gömb
• 5. módszer a 7-ből: Henger
• 6. módszer a 7-ből: Négyzet alakú piramis
• 7/7 módszer: Kúp
• Szükségletek

A terület az objektum összes területe által elfoglalt teljes terület. Ez az objektum összes területének összege. A háromdimenziós alakzat területének megtalálása meglehetősen egyszerű, amennyiben a megfelelő képletet használja. Minden alaknak megvan a maga külön képlete, ezért először meg kell találnia, hogy melyik alakzatról van szó. A különböző objektumok területképletének kiszámítása megkönnyítheti a jövőben a számításokat. Itt megvitatjuk a leggyakoribb formákat, amelyekkel találkozhat.

Lépni

1. módszer a 7-ből: Kocka

1. Határozza meg a kocka területének képletét. Egy kocka hat egyforma arccal rendelkezik. Mivel a négyzet hossza és szélessége egyaránt megegyezik, a négyzet területe is a, ahol a a hossza az egyik oldala. Mivel egy kockának hat egyenlő arca van, kiszámíthatja annak területét úgy, hogy megszorozza az egyik oldal területét hatmal. A kocka területének képlete O O = 6a, ahol a a hossza az egyik oldala.
   • A területegységek egy meghatározott hosszúság négyzetben vannak: cm, dm, m stb.
2. Mérje meg az egyik oldal hosszát. A kocka mindkét oldalának vagy élének definíció szerint meg kell egyeznie a másikkal, ezért csak az egyik oldalát kell megmérnie. Mérje meg az oldal hosszát vonalzóval. Ügyeljen a használt egységekre.
   • Jegyezzük fel ezt a mérést a.
   • Példa: a = 2 cm
3. Szögezze le a mérését a. A borda hosszának kiszámításához jelölje be négyzetbe a mérést. Az érték négyzetbe foglalása magában foglalja annak szorzását. Ha ezt először tanulja, akkor hasznos lehet ezt megjegyezni SA = 6 * a * a.
   • Vegye figyelembe, hogy ez a lépés kiszámítja a kocka egyik oldalának területét.
   • Példa: a = 2 cm
   • a = 2 x 2 = 4 cm
4. Szorozza meg ezt a terméket hatmal. Ne felejtsük el, hogy egy kockának hat azonos arca van. Most, hogy ismeri az egyik arc területét, szorozza meg hatmal (mind a hat arc miatt).
   • Ez a lépés befejezi a kocka területének kiszámítását.
   • Példa: a = 4 cm
   • Terület = 6 x a = 6 x 4 = 24 cm

2. módszer a 7-ből: Téglalap alakú prizma

1. Határozza meg a téglalap alakú prizma területének képletét. Mint egy kocka, a téglalap alakú prizma is hat arccal rendelkezik, de a kockával ellentétben ezek az arcok nem azonosak. Téglalap alakú prizmával csak az ellenkező oldalak egyenlőek egymással. Ezért egy téglalap alakú prizma területének kiszámításakor figyelembe kell venni a bordák különböző hosszúságait, mint a képletben SA = 2ab + 2bc + 2ac.
   • Ehhez a képlethez a egyenlő a prizma szélességével, b megegyezik a magassággal és c megegyezik a hosszúsággal.
   • Ha jobban megnézzük a képletet, akkor látni fogja, hogy egyszerűen hozzáadjuk az objektum minden arcának minden területét.
   • A terület egysége egy bizonyos hosszúságú négyzet lesz: cm, dm, m stb.
2. Mérje meg mindkét oldal hosszát, magasságát és szélességét. Mindhárom leolvasás eltérhet, ezért mindegyiket egyenként kell mérni. Mérje meg mindkét oldalt egy vonalzóval, és rögzítse az értéket. Minden mérésnél ugyanazokat az egységeket használja.
   • Mérje meg és rendelje hozzá az alap hosszát a prizma hosszának meghatározásához c.
   • Példa: c = 5 cm
   • Mérje meg és nevezze meg az alap szélességét a prizma szélességének meghatározásához a.
   • Példa: a = 2 cm
   • Mérje meg és nevezze meg az oldal magasságát a prizma magasságának meghatározásához b.
   • Példa: b = 3 cm
3. Számítsa ki a prizma egyik arcának területét, és szorozza meg kettővel. Ne feledje, hogy egy téglalap alakú prizmában hat arc van, és az ellenkező arcok egyenlőek egymással. Szorozzuk meg a hosszúságot és a magasságot, ill c és a, hogy megtalálja a sík területét. Hajtsa végre ezt a mérést, és szorozza meg kettővel az ellentétes azonos sík számításához.
   • Példa: 2 x (a x c) = 2 x (2 x 5) = 2 x 10 = 20 cm
4. Keresse meg a prizma másik arcának területét, és szorozza meg kettővel. Az első arckészlethez hasonlóan szorozza meg a szélességet és a magasságot, ill a és b a prizma másik arcának területének meghatározásához. Szorozza meg ezt a mérést kettővel az ellentétes azonos oldalak kiszámításához.
   • Példa: 2 x (a x b) = 2 x (2 x 3) = 2 x 6 = 12 cm
5. Számítsa ki a prizma végeinek területét, és szorozza meg kettővel. A prizma másik két arca a vége. Szorozzuk meg a hosszúságot és a szélességet (c és b), hogy megtalálják a felületüket. Szorozza meg ezt a területet kettővel, hogy mindkét oldal figyelembe vehesse.
   • Példa: 2 x (b x c) = 2 x (3 x 5) = 2 x 15 = 30 cm
6. Adja össze a három különálló területet. Mivel a prizma területe az objektum összes arcának teljes területe, az utolsó lépés az összes egyedileg kiszámított terület összeadása. Adja hozzá az összes oldalon lévő területeket a teljes területhez.
   • Példa: Terület = 2ab + 2bc + 2ac = 12 + 30 + 20 = 62 cm.

3. módszer a 7-ből: Háromszög alakú prizma

1. Határozza meg a háromszög alakú prizma területképletét. A háromszög alakú prizmának két egyforma háromszög és három téglalap alakú oldala van. A terület megtalálásához ki kell számolnia az összes arc területét, és össze kell adnia őket. A háromszög alakú prizma területe SA = 2A + PH, ahol A a háromszög alakú alap területe, P a háromszög alakú alap kerülete és h a prizma magassága.
   • Ez vonatkozik erre a képletre a egy háromszög területe és így A = 1/2 melltartó, ahol b a háromszög alapja és h a magasság.
   • P. a háromszög kerülete a háromszög mindhárom élének összeadásával számítva.
   • A terület egységei a négyzet hosszának egységei: cm, dm, m stb.
2. Számítsa ki a háromszög alakú felület területét, és szorozza meg kettővel. A háromszög területe:₂b * h ahol b a háromszög alapja és h a magasság. Mivel két egyforma háromszög van arcként, a képletet megszorozzuk kettővel. Ez megkönnyíti a számítást mindkét síkon (b * h).
   • Az alap b, egyenlő a háromszög aljának hosszával.
   • Példa: b = 4 cm
   • A magasság h A háromszög alapja megegyezik az alsó él és a hegy közötti távolsággal.
   • Példa: h = 3 cm
   • Egy háromszög területe szorozva 2 = 2 (1/2) b * h = b * h = 4 * 3 = 12 cm
3. Mérjük meg a háromszög mindkét oldalát és a prizma magasságát. A területszámítás befejezéséhez ismernie kell a háromszög mindkét oldalának hosszát és a prizma magasságát. A magasság a két háromszög alakú oldal közötti távolság.
   • Példa: H = 5 cm
   • A három oldal a háromszög alakú alap három oldalára utal.
   • Példa: S1 = 2 cm, S2 = 4 cm, S3 = 6 cm
4. Keresse meg a háromszög kerületét. A háromszög kerülete az összes mért oldal összeadásával kiszámítható: S1 + S2 + S3.
   • Példa: P = S1 + S2 + S3 = 2 + 4 + 6 = 12 cm
5. Szorozzuk meg az alap kerületét a prizma magasságával. Ne feledje, hogy a prizma magassága a két háromszög alakú oldal közötti távolság. Más szavakkal: szaporodjon P. val vel H.
   • Példa: P x H = 12 x 5 = 60 cm
6. Adja össze a két külön olvasatot. Összeadnia kell az előző két lépés két mérését a háromszög alakú prizma területére.
   • Példa: 2A + PH = 12 + 60 = 72 cm.

4/7 módszer: Gömb

1. Határozza meg a gömb területképletét. Egy gömbnek ívelt területe van, ezért a területe egy érték, szorozva a pi állandóval. A gömb területét az egyenletből számoljuk SA = 4π * r.
   • Ehhez a képlethez r egyenlő a gömb sugarával. Pi (vagy π) 3,14-re kerekíthető.
   • A terület egységei hosszúsági egységek lesznek, négyzetben: cm, dm, m stb.
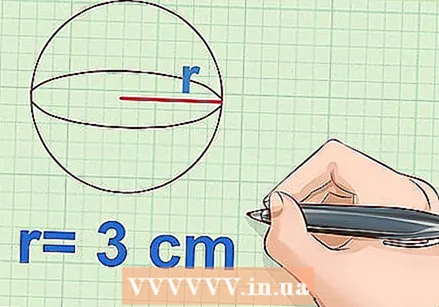2. Mérje meg a sugarat a gömb. A gömb sugara az átmérő fele, vagy a gömb közepétől a széléig terjedő távolság.
   • Példa: r = 3 cm
3. Szögezze be a sugarat. A szám négyzetbe állításához meg kell szorozni önmagával. Szorozza meg a r önmagával. Ne feledje, hogy ezt a képletet SA = 4π * r * r néven írhatjuk át.
   • Példa: r = r x r = 3 x 3 = 9 cm
4. Szorozza meg a négyzet sugarát egy kerekítéssel pi. A Pi egy állandó, amely a kör kerületének és az átmérőjének arányát képviseli. Ez irracionális szám, sok tizedesjegyű. Gyakran kerekítik 3,14-re. Szorozzuk meg a négyzet sugarát π-vel vagy 3,14-gyel a gömb kör alakú szakaszának területére.
   • Példa: π * r = 3,14 x 9 = 28,26 cm
5. Szorozza meg ezt a terméket néggyel. A számítás befejezéséhez szorozzuk meg néggyel. Keresse meg a gömb területét úgy, hogy megszorozza a lapos kör alakú négyet.
   • Példa: 4π * r = 4 x 28,26 = 113,04 cm

5. módszer a 7-ből: Henger

1. Határozza meg a henger területképletét. A hengernek két kör alakú vége van, amelyek lezáródnak egy cső alakú felületről. A henger területének képlete: SA = 2π * r + 2π * rh, ahol r megegyezik a kör alakú alap sugarával és h megegyezik a henger magasságával. kerek pi (vagy π) 3,14-re csökken.
   • A 2π * r képlet kiszámítja a két kör alakú terület területét, míg a 2πrh az oszlop területe a két vég között.
   • A területegységek a négyzet hosszának egységei: cm, dm, m stb.
2. Mérjük meg a henger sugarát és magasságát. A kör sugara átmérőjének fele, vagy a kör közepétől a széléig terjedő távolság. A magasság a henger egyik végétől a másikig terjedő teljes távolsága. Rajzolja le és rögzítse ezeket a méréseket vonalzóval.
   • Példa: r = 3 cm
   • Példa: h = 5 cm
3. Keresse meg az alap területét és szorozza meg kettővel. Az alap területének megkereséséhez használja a terület vagy egy kör képletét (π * r). A számítás befejezéséhez szögeltesse be a sugarat és szorozza meg pi. Ezután szorozzuk meg kettővel a henger másik végén lévő második azonos kör miatt.
   • Példa: Az alap területe = π * r = 3,14 x 3 x 3 = 28,26 cm
   • Példa: 2π * r = 2 x 28,26 = 56,52 cm
4. Számítsa ki maga a henger területét 2π * rh-val. Ez a képlet a cső területének kiszámításához. A cső a henger két kör alakú vége közötti tér. Szorozza meg a sugarat kettővel, pi és a magasság.
   • Példa: 2π * rh = 2 x 3,14 x 3 x 5 = 94,2 cm
5. Adja össze a két külön olvasatot. A henger teljes területének kiszámításához adja hozzá a két kör területét a két kör közötti tér területéhez. Megjegyzés: a két darab hozzáadásakor felismeri az eredeti képletet: SA = 2π * r + 2π * rh.
   • Példa: 2π * r + 2π * rh = 56,52 + 94,2 = 150,72 cm

6. módszer a 7-ből: Négyzet alakú piramis

1. Határozza meg a négyzet alakú piramis területképletét. A négyzet alakú piramisnak négyzet alakú alapja és négy háromszög alakú oldala van. Mint említettük, egy négyzet területe az egyik oldal négyzetének hossza. A háromszög területe 1 / 2sl (a háromszög oldala a háromszög hosszának vagy magasságának a szorosa). Mivel négy háromszög van, kiszámítja a teljes területet, megszorozva azt néggyel. Ha ezeket az arcokat összeadjuk, megkapjuk a négyzet alakú piramis területének egyenletét: SA = s + 2sl.
   • Ebben az egyenletben s a négyzet alakú alap mindkét oldalának hossza és l az egyes háromszögek oldalának ferde magassága.
   • A terület egysége egy meghatározott négyzetnyi hosszegység: cm, dm, m stb.
2. Mérje meg a ferde magasságot és az alapoldalt. A ferde magasság l, az egyik háromszög alakú oldal magassága. Ez a piramis aljától a csúcsáig tartó távolság, amelyet egy lapos oldalon mérnek. Az alapoldal s, a négyzet alakú alap egyik oldalának hossza. Mivel az alap négyzet alakú, ez a mérés minden oldalon megegyezik. Minden méréshez használjon vonalzót.
   • Példa: l = 3 cm
   • Példa: s = 1 cm
3. Határozza meg a négyzet alakú alap területét. A négyzet alakú alapterület kiszámítható az oldal hosszának négyzetesével (s megszorozza magát).
   • Példa: s = s x s = 1 x 1 = 1 cm
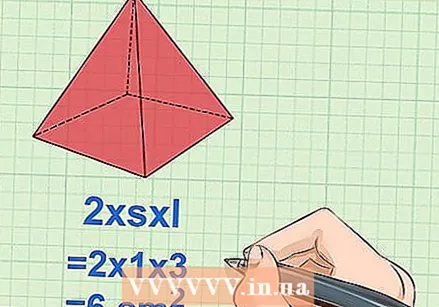4. Számítsa ki a négy háromszög alakú oldal teljes területét. Az egyenlet második része a másik négy háromszög felületének területe. A 2ls képlet segítségével megszorozzuk s val vel l és kettő. Ez megtalálja az egyes arcok területét.
   • Példa: 2 x s x l = 2 x 1 x 3 = 6 cm
5. Adja össze a két különálló területet. A teljes terület kiszámításához adja hozzá az arcok teljes területét az alap területéhez.
   • Példa: s + 2sl = 1 + 6 = 7 cm

7/7 módszer: Kúp

1. Határozza meg a kúp területképletét. A kúpnak kör alakú alapja és lekerekített felülete van, amely egy pontig keskenyedik. A terület megkereséséhez vegye fel a kör alakú alap és a kúp területét, és adja hozzá a kettőt. A kúp területének képlete: SA = π * r + π * rl, ahol r a kör alakú alap sugara, l a kúp ferde magassága, és π a pi állandó értéke (3,14).
   • A terület egysége egy meghatározott négyzet alakú egység: cm, dm, m stb.
2. Mérje meg a kúp sugarát és magasságát. A sugár a kör alakú alap közepétől az alap széléig terjedő távolság. A magasság az alap közepétől a kúp hegyéig terjedő távolság, a kúp közepén keresztül mérve.
   • Példa: r = 2 cm
   • Példa: h = 4 cm
3. Számítsa ki a ferde magasságot (l) a kúp. Mivel a ferde magasság a háromszög tényleges hipotenúza, ennek kiszámításához a Pitagorasz-tételt kell használnia. Használja az átrendezett űrlapot, l = √ (r + h), ahol r a sugár és h a kúp magassága.
   • Példa: l = √ (r + h) = √ (2 x 2 + 4 x 4) = √ (4 + 16) = √ (20) = 4,47 cm
4. Keresse meg a kör alakú alap területét. Az alap területét a π * r képlettel számoljuk. A sugár megmérése után négyzetre állítja (megszorozza önmagával), majd megszorozza azt a szorzatot pi-vel.
   • Példa: π * r = 3,14 x 2 x 2 = 12,56 cm
5. Számítsa ki a kúp tetejének területét. Használja a π * rl képletet, ahol r a kör sugara és l a kúp tetejének területének meghatározásához a fent leírt lejtés.
   • Példa: π * rl = 3,14 x 2 x 4,47 = 28,07 cm
6. Adja össze a két területet, hogy megkapja a kúp teljes területét. Számítsa ki a kúp végső területét úgy, hogy hozzáadja a kör alakú terület területét az előző lépésből származó számításhoz.
   • Példa: π * r + π * rl = 12,56 + 28,07 = 40,63 cm

Szükségletek

• Vonalzó
• Toll vagy ceruza
• Papír