Tartalom

• Lépések
• 1. módszer a 3 -ból: 1. rész: Az inflexiós pont meghatározása
• 2. módszer a 3 -ból: Egy függvény származékainak kiszámítása
• 3. módszer a 3 -ból: 3. rész: Keresse meg az inflexiós pontot
• Tippek

Differenciálszámításban az inflexiós pont egy görbe azon pontja, ahol görbülete előjelet vált (pluszról mínuszra vagy mínuszról pluszra). Ezt a koncepciót használják a gépiparban, a gazdaságban és a statisztikákban az adatok jelentős változásainak azonosítására.

Lépések

1. módszer a 3 -ból: 1. rész: Az inflexiós pont meghatározása

1. 1 A homorú függvény meghatározása. A konkáv függvény gráfjának bármelyik akkordja (két pontot összekötő szegmens) közepe vagy a grafikon alatt, vagy azon található.
2. 2 Konvex függvény meghatározása. A domború függvény grafikonjának bármelyik akkordja (két pontot összekötő szegmens) közepe vagy a grafikon felett, vagy azon található.
3. 3 A függvény gyökereinek meghatározása. A függvény gyökere az "x" változó értéke, amelynél y = 0.
   • Egy függvény ábrázolásakor a gyökerek azok a pontok, amelyeken a gráf keresztezi az x tengelyt.

2. módszer a 3 -ból: Egy függvény származékainak kiszámítása

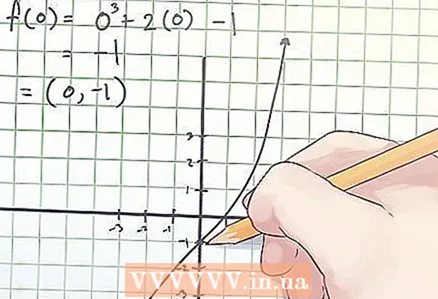
1. 1 Keresse meg a függvény első deriváltját. Nézze meg a differenciálás szabályait a tankönyvben; meg kell tanulnia az első derivátumok felvételét, és csak ezután léphet a bonyolultabb számításokhoz. Az első deriváltokat f '(x) jelöléssel látjuk el. Az ax ^ p + bx ^ (p - 1) + cx + d alakú kifejezéseknél az első derivált: apx ^ (p - 1) + b (p - 1) x ^ (p - 2) + c.
   • Például keressük meg az f (x) = x ^ 3 + 2x -1 függvény inflexiós pontjait. Ennek a függvénynek az első deriváltja:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Keresse meg a függvény második deriváltját. A második derivált az eredeti függvény első deriváltjának származéka. A második deriváltot f ′ ′ (x) jelöléssel látjuk el.
   • A fenti példában a második derivált:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Állítsa a második deriváltot nullára, és oldja meg a kapott egyenletet. Az eredmény a várható inflexiós pont lesz.
   • A fenti példában a számítás így néz ki:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Keresse meg a függvény harmadik deriváltját. Annak ellenőrzésére, hogy az eredmény valójában inflexiós pont, keresse meg a harmadik deriváltot, amely az eredeti függvény második deriváltjának származéka. A harmadik deriváltot f ′ ′ ′ (x) jelöléssel látjuk el.
   • A fenti példában a harmadik derivált:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

3. módszer a 3 -ból: 3. rész: Keresse meg az inflexiós pontot

1. 1 Nézze meg a harmadik származékot. Az inflexiós pont becslésének általános szabálya az, hogy ha a harmadik derivált nem nulla (azaz f ′ ′ ′ (x) ≠ 0), akkor az inflexiós pont az igazi inflexiós pont. Nézze meg a harmadik származékot; ha nem nulla, akkor megtalálta az igazi inflexiós pontot.
   • A fenti példában a harmadik derivált 6, nem 0.Tehát megtalálta az igazi inflexiós pontot.
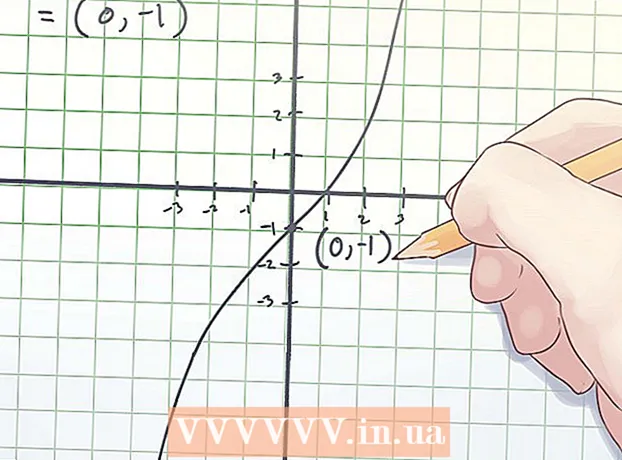
2. 2 Keresse meg az inflexiós pont koordinátáit. Az inflexiós pont koordinátáit (x, f (x)) jelöljük, ahol x az "x" független változó értéke az inflexiós ponton, f (x) a függő "y" változó értéke az inflexiónál pont.
   • A fenti példában, amikor a második deriváltot nullával egyenlítettük ki, azt találtuk, hogy x = 0. Tehát, hogy meghatározzuk az inflexiós pont koordinátáit, keressük meg az f (0) értéket. A számításod így néz ki:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
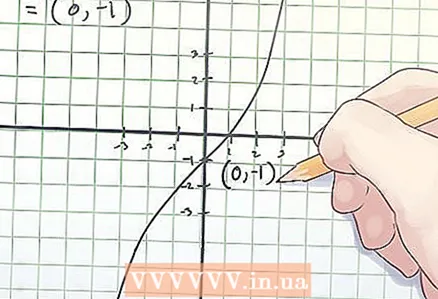3. 3 Írja le az inflexiós pont koordinátáit! Az inflexiós pont koordinátái a talált x és f (x) értékek.
   • A fenti példában az inflexiós pont a (0, -1) koordinátákon található.

Tippek

• A szabad kifejezés (prímszám) első deriváltja mindig nulla.